An Optimization Scheme for Non-negative Matrix Factorization under Probability Constraints

Hiroyoshi Ito, Graduate School of Systems and Information Engineering, University of Tsukuba, Tsukuba, Japan
Toshiyuki Amagasa, Center for Computational Sciences, University of Tsukuba, Tsukuba, Japan

Abstract

Non-negative matrix factorization (NMF) has been recognized as an effective method of dimensionality reduction over matrices and has been successfully applied for wide variety of tasks in different domains, such as text, image, and audio. In many cases, such matrices represent probabilities of the modeled objects while standardized optimization algorithms for NMF did not take into account the probabilistic constraints. In this paper we propose a novel optimization algorithm for NMF under probability constraints, thereby achieving better performance in terms of accuracy without losing efficiency. More precisely, our theoretical analysis of our algorithm shows that: (1) our method monotonically decreases the objective function; (2) the output matrices satisfy the probability constraint; (3) its learning rate is the largest while among satisfying (1) and (2); and (4) the computational time complexity remains the same as the existing optimization method. We conduct experimental evaluations using a real-world dataset by applying the proposed method to different tasks. The results show that, when applying it to topic modeling, the accuracy of clustering and topic detection is better than the ordinary NMF. When applying it to an algorithm for community detection and attribute-value clustering over multi-attributed graphs (CARNMF [1]), it also achieved higher accuracy compared to the original NMF optimization.

Index Terms — Non-negative Matrix Factorization, Optimization, Topic model

I. INTRODUCTION

Non-negative matrix factorization (NMF) is a method that approximates a non-negative matrix by the product of two low-rank non-negative matrices [2], [3]. Due to its efficiency and effectiveness, NMF is widely used for different types of data analysis, such as document clustering [4], [5] and topic detection [6]–[8] over document data, community detection over graph data [9]–[12], audio signal analysis [13], and image processing [3]. Moreover, several studies have shown that combining multiple NMF tasks could contribute to improving the output quality [1], [6], [14]–[16].

It should be noticed that, in many data analysis tasks, probabilistic interpretation of models plays an important role due to the fact that probability allows us to explicitly explain the generative process of the observed data, which could lead to interpretable model generation as well. In particular, probabilistic interpretation is a quite powerful tool when combining different tasks, because it allows us to deal with completely different models in terms of probability. In fact, several previous studies, where multiple NMF tasks are combined, have attempted to give an interpretation of probability of input and output matrices [1], [14], [15].

However, the optimization methods in these studies do not pay attention to the probabilistic constraint in a matrix, i.e., a probability is a non-negative value which is less than 1.0 and the sum of all probabilities is equal to 1.0. Instead, when performing NMF, updated matrices do not meet probabilistic constraints, which are in turn forced to satisfy the constraints by applying normalization. As can easily be conjectured, it would be desirable and beneficial as well if optimization of multiple NMF tasks can be performed in such a way that probabilistic constraints are naturally integrated.

In this paper, we propose a novel optimization method for NMF under probabilistic constraint, which is called probabilistic NMF, whereby the output matrices are interpretable as probability matrices without any operation such as normalization. Specifically, we exploit topic modeling as an example of probabilistic NMF and derive an optimization scheme for it. The loss function is formulated as difference between document-term matrix (each element indicates the joint probability of presence of a document and a term) and multiplication of document-topic matrix (each element indicates the joint probability of presence of a document and a topic) and topic-term matrix (each element indicates the conditional probability of presence of a term given a topic). We derive iterative updating rules for the output matrices based on Karush-Kuhn-Tucker (KKT) conditions of non-negativity and equality constraints for probability interpretation of the output matrices.

In addition, we examine the usefulness of our optimization scheme with a more complicated model based on NMF and applying the interpretation of probability for output matrices. More precisely, we apply this method to the loss function of CARNMF [1], which can perform community detection and attribute-value clusterings over multi-attributed graphs at the same time. The loss function of CARNMF consists of multiple types of NMF loss functions, i.e., community detection, detection of attribute clusters and detection of relevance between communities and attribute-value clusters. Note that, in the original method, the optimization method does not takeinto account probabilistic constraints; i.e., it could not fully take advantage of the mutual complement of different NMF tasks. To this problem, in this research, we examine the effect of applying this optimization method to this problem.

The key contributions of this research can be summarized as follows:

We propose a novel method for optimizing NMF under probabilistic constraint, probabilistic NMF, which yields probabilistically interpretable matrices. For the method, we give theoretical supports for the validity of update rules: (1) our optimization scheme monotonically decrease the objective function; (2) the output matrices always meet the probability constraints; (3) the learning rate of update rules for each output matrix is the maximum among satisfying (1) and (2); and (4) the time complexity of the proposed optimization scheme remains the same as the ordinary NMF.
The experimental results show that, when applying it to topic modeling under probabilistic NMF, the model optimized by our optimization scheme is more accurate than the ordinary NMF regarding clustering and topic detection without sacrificing efficiency compared with ordinary NMF.
Another experimental results regarding CARNMF show that we achieve more accurate communities and attribute-value clusters than the original optimization algorithm.

Non-negative matrix factorization (NMF) is used to decompose an input non-negative matrix into two non-negative matrices with lower rank. Lee et al. [2] proposed an efficient optimization algorithm for NMF, which formed a foundation for the subsequent research works based on NMF. In fact, NMF has been shown to be useful in various tasks. Xu et al. [4] showed that NMF is effective for document clustering. Guillamet and Vitria [17] showed that NMF based feature detection is effective for face recognition task. Wang et al. [12] developed an NMF based community detection method for graph data and revealed that the method is effective for overlapping community detection. Note here that it has been proven by many research works that NMF show good performance on topic modeling tasks.

For more complicated tasks, several studies have shown that concurrent processing of two or more NMF tasks is useful to improve the output performance. Wang et al. [14] showed that, by solving NMF of community detection and detecting attributes of communities from an attributed network, the quality of detected community could be improved. Liu et al. [16] proposed multi-view clustering scheme based on multiple NMFs for multi-view data. In our previous work, we proposed an NMF based clustering scheme for multi-attributed graph called CARNMF [1], which outputs community detection, attribute-value clustering, and derivation of relationships between communities and attribute-value clusters at the same time. Notice that all of these researches assume probabilistic interpretation on the output matrices, thereby enabling integration of different types of data. However, none of the above studies guarantee that output matrices satisfy the probability constraints and/or the optimization method is exclusively dedicated for the problem being addressed in the respective paper and is therefore not applicable to other problems.

Several works have studied how NMF can be applied to stochastic models. Studies in Ding et al. [18], [19], and Gaussier and Goutte [20] revealed that the loss function of NMF under KL-divergence is equivalent to the loss function of pLSI. Although NMF under KL-divergence inherits probabilistic interpretation on output matrices, it is known that the optimization algorithm for the loss function are much slower than those for frobenius norm based NMF. Luo et al. [21] proposed probabilistic NMF for topic modeling that directly approximates the input probabilistic matrix by the product of output probabilistic matrices with low rank. However, the proposed optimization algorithm needs iterative updating for each output matrix in addition to the outer iteration, which makes the number of calculation much larger than the ordinary NMF. By contrast, as we will see later, the computational complexity of our proposed optimization scheme the same to the ordinary NMF and also the learning speed is comparable. Moreover, our optimization scheme is widely applicable to other problems that exploit probabilistic matrix.

III. PROBLEM DEFINITION

In this study, we propose an optimization scheme for non-negative matrix factorization (NMF) under probabilistic constraints where each output matrix is constrained to be stochastic; i.e., each element is a non-negative real number representing probability. Hereafter, we call it \(\textit{probabilistic NMF}\). In this paper, we exploit topic modeling over documents as an easy-to-understand example to derive optimization for loss function.
However, the proposed scheme is not limited to topic modeling and can be applied to other problems as long as it is based on probabilistic representations of matrices.

First, we give a formulation of loss function for topic modeling under probabilistic NMF. Given a set of documents, we represent them using a document-term matrix \(X\in {\mathbb R}^{N \times M}\), where \(N\) is the number of documents and \(M\) is the length of a dictionary. We normalize \(X\) as \(\sum_{i,j}X_{i,j}=1\) so that each element \(X_{d,w}\) in matrix \(X\) represents the joint probability \(p(d, w)\) of document \(d\) and word \(w\) in the input document. In the probabilistic NMF based topic modeling, the ratio of the topic of the document is represented by a matrix \(U \in {\mathbb R}^{N \times K}\), where \(K\) is the number of topics satisfying \(K \ll M\). The rows and columns of matrix \(U\) denote documents and topics, respectively. Each element \(U_{d,z}\) of the matrix represents the joint probability \(p(d, z)\) of document \(d\) and topic \(z\). Also, the probability distribution of words in the topic is represented by a matrix \(V\in {\mathbb R}^{K \times M}\). Similarly, the rows and columns of matrix \(V\) denote topics and words, respectively. Each element \(V_{z,w}\) of the matrix represents the conditional probability \(p(w|z)\), i.e., the appearance of word \(w\) given topic \(z\). In probability \(p(d,z,w)\), document \(d\) has word \(w\) through topic \(z\) which is represented by \(U_{d,z}V_{z,w}=p(d,z)p(w|z)=p(d,z,w)\). Furthermore, the joint probability \(p(d,w)\), which is equal to \(X_{d,w}\), is expressed by \(\sum_{z}U_{d,z}V_{z,w}=\sum_{z}p(d,z,w)=p(d,w)\). By using frobenius norm as a function to evaluate the difference, the optimization problem is expressed as follows:

\begin{align} \argmin _{U, V \geq 0}~ &L= \left\lVert X-UV^T \right\rVert ^2_F \\ \end{align} subject to \(\sum_{i,j} U_{ij}=1, \nonumber\) \( \sum_{l}V_{kl} = 1,~ \forall k \nonumber. \)

This optimization problem is formulated as a minimization problem under two types of the constraints: inequality constraints as non-negativity constraints, equality constraints as the probability constraints. By solving this problem, the most reasonable topic model can be estimated, thereby making it possible for us to get an interpretation of the probability to the output matrices \(U\) and \(V\).

IV. OPTIMIZATION

In this section, we propose an optimization scheme for the problem described in the previous section. Similar to the ordinary NMF, the loss function \(L\) is convex with respect to each output matrix (\(U\) or \(V\)) but is not when considering both output matrices at the same time. In this paper, we propose iterative update rules for \(U\) and \(V\) whereby the output matrices are alternately adjusted while optimizing the loss function \(L\). However, unlike the ordinary NMF, our probabilistic NMF has equality constraints as the probability constraints on \(U\) and \(V\), leading to a more complicated optimization problem. To tackle this problem, we employ Karush-Kuhn-Tucker (KKT) condition to derive the update rules for each matrix \(U\) and \(V\). In the KKT conditions, the Lagrange multipliers are introduced for the equality constraints in addition to the non-negativity constraints, which must be determined. As a result, by determining the Lagrange multipliers for non-negativity and equality constraints, we derive the following update rules:

\begin{align} U_{ij}^{\prime} \gets~& U_{ij}~ \frac {\left[\partial_{U_{ij}}L\right]^- + \lambda^{-}} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}},\\ &\lambda^{-} = \frac {1-\sum_{i,j} \frac {U_{ij}\left[\partial_{U_{ij}}L\right]^-} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}}} {\sum_{i,j} \frac {U_{ij}} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}},}\\ &\lambda^{+} = \max\left(\max\left( -\partial_{U_{\cdot,\cdot}}L \right),0\right),\\ V_{kl}^{\prime} \gets~&V_{kl}~ \frac {[\partial_{V_{kl}}L]^- + \psi_{k}^{-}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}},\\ &\psi_k^{-} = \frac {1-\sum_{l} \frac {V_{kl}\left[\partial_{V_{kl}}L\right]^-} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}}} {\sum_{l} \frac {V_{kl}}{\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}}},\\ &\psi_k^{+} = \max\left(\max\left( -\partial_{V_{k\cdot}}L \right),0\right), \end{align} where \begin{align} \partial_{U_{ij}}L &= \left[\partial_{U_{ij}}L\right]^+ - \left[\partial_{U_{ij}}L\right]^-, \nonumber \\ &\left[\partial_{U_{ij}}L\right]^- = \left(XV^T\right) {ij},~ \left[\partial_{U_{ij}}L\right]^+ = (UVV^T) {ij}, \nonumber \\ \partial_{V_{kl}}L &= \left[\partial_{V_{kl}}L\right]^+ - \left[\partial_{V_{kl}}L\right]^-. \nonumber \\ &\left[\partial_{V_{kl}}L\right]^- = (U^TX) {kl},~ \left[\partial_{V_{kl}}L\right]^+ = (U^TUV) {kl}. \nonumber \end{align}

These update rules monotonically decrease the loss function under satisfying the constraints. From the following subsections, we will describe the derivation process of each update rule and theoretical supports of validity about update rules.

A. Derivation of update rules

Based on KKT condition, we introduce Lagrange multiplier matrices \(\Theta = (\theta_{ij})\) and \(\Xi = (\xi_{kl})\) for non-negative constraint of \(U_{ij}\) and \(V_{kl}\), respectively, and Lagrange multipliers \(\lambda\) and \(\Psi = (\psi_{i})\) for equality constraint of \(U_{ij}\) and \(V_{kl}\), respectively.

We have the following equivalent objective functions: \begin{align} {\mathcal L}(U_{ij}) &= L + \sum_{i,j}\theta_{ij}U_{ij} + \lambda \left(\sum_{i,j}U_{ij}-1\right),\\ {\mathcal L}(V_{kl}) &= L + \sum_{k,l}\xi_{kl}V_{kl} + \sum_{k}\psi_{k}\left(\sum_{l}V_{kl}-1\right). \end{align}

Set derivative of \({\mathcal L}(U_{ij})\) with respect to \(U_{ij}\), and \({\mathcal L}(V_{kl})\) with respect to \(V_{kl}\) to \(0\), we have: \begin{align} \partial_{U_{ij}}{\mathcal L}(U_{ij}) &= \partial_{U_{ij}}L + \theta_{ij} + \lambda =0,\\ \partial_{V_{kl}}{\mathcal L}(V_{kl}) &= \partial_{V_{kl}}L + \xi_{kl} + \psi_{k} =0. \end{align}

Following the KKT condition for the non-negativity of \(U_{ij}\), and \(V_{kl}\), we have the following equations: \begin{align} U_{ij} \theta_{ij} &= U_{ij} \left( -\partial_{U_{ij}}L - \lambda \right) =0,\\ V_{kl}\xi_{kl} &= V_{kl} \left( - \partial_{V_{kl}}L - \psi_k \right) =0. \end{align}

Let \(\partial_{U_{ij}}L = \left[\partial_{U_{ij}}L\right]^+ - \left[\partial_{U_{ij}}L\right]^-\) and \(\lambda=\lambda^+ - \lambda^-\), where \(\left[\partial_{U_{ij}}L\right]^+ \geq 0\), \(\left[\partial_{U_{ij}}L\right]^- \geq 0\), \(\lambda^+ \geq 0\), and \(\lambda^- \geq 0\), the equation 12 is equivalent to:

\begin{align} U_{ij}\left( \left[\partial_{U_{ij}}L\right]^+ - \left[\partial_{U_{ij}}L\right]^- +\lambda^{+} - \lambda^{-}\right) =0. \end{align}

Similarly, let \(\partial_{V_{kl}}L = \left[\partial_{V_{kl}}L\right]^+ - \left[\partial_{V_{kl}}L\right]^-\) and \(\psi_k=\psi_k^+ - \psi_k^-\), where \(\left[\partial_{V_{kl}}L\right]^+ \geq 0\), \(\left[\partial_{V_{kl}}L\right]^- \geq 0\), \(\psi_k^+ \geq 0\), and \(\psi_k^- \geq 0\), the equation 13 is equivalent to:

\begin{align} V_{kl} \left( \left[\partial_{V_{kl}}L\right]^+ - \left[\partial_{V_{kl}}L\right]^- + \psi_k^{+} - \psi_k^{-}\right) =0. \end{align} These are the fixed point equations that the solutions must satisfy at convergence. Given an initial value of \(U_{ij}\) and \(V_{kl}\), we can get the following update rules:

\begin{align} U_{ij}^{\prime} &\gets U_{ij} \frac {\left[\partial_{U_{ij}}L\right]^- + \lambda^{-}} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}},\\ V_{kl}^{\prime} &\gets V_{kl} \frac {\left[\partial_{V_{kl}}L\right]^- + \psi_k^{-}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}}. \end{align}

Next, we determine the Lagrange multipliers \(\lambda\) and \(\psi_k\) for equality constraints \(\sum_{i,j}U_{ij} = 1\) and \(\sum_{l}V_{kl} = 1\). \(\lambda^{+}\), \(\lambda^{-}\), \(\psi_i^{+}\), and \(\psi_i^{-}\) must satisfy following equations: \begin{align} \sum_{i,j}{U_{ij}^{\prime}} &= \sum_{i,j} U_{ij} \frac {\left[\partial_{U_{ij}}L\right]^- + \lambda^{-}} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}} = 1,\\ \sum_{l}{V_{kl}^{\prime}} &= \sum_{l} V_{kl} \frac {\left[\partial_{V_{kl}}L\right]^- + \psi_k^{-}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}} = 1 \end{align} which are equivalent to:

\begin{align} \sum_{i,j} \frac {U_{ij} \left[\partial_{U_{ij}}L\right]^- } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } +\lambda^{-} \sum_{i,j} \frac {U_{ij}} { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } = 1,\\ \sum_{l} \frac { V_{kl} \left[\partial_{V_{kl}}L\right]^- } { \left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}} +\psi_k^{+} \sum_{l} \frac {V_{kl}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}} = 1. \end{align} From Equations 22 and 23, let \(\lambda^{+}\) and \(\psi^{+}_k\) be the parameters of \(\lambda^{-}\) and \(\psi^{-}_k\), respectively. With the constraints \(\lambda^{+},\lambda^{-},\psi^{+}_k,\psi^{-}_k\geq 0\), we have the following inequalities: \begin{align} \lambda^{-} = \frac {1 - \sum_{i,j} \frac {U_{ij} \left[\partial_{U_{ij}}L\right]^-} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}} } {\sum_{i,j} \frac {U_{ij}} {\left[\partial_{U_{ij}}L\right]^+ +\lambda^{+}} } \geq 0, \\ \lambda^{+} \geq 0, \\ \psi_k^{-} = \frac {1 - \sum_{l} \frac { V_{kl} \left[\partial_{V_{kl}}L\right]^- } { \left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}} } {\sum_{l} \frac {V_{kl}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}}} \geq 0, \\ \psi^{+} \geq 0. \end{align} Under satisfying inequalities 22 and 23, the updated \(U_{ij}^{\prime}\) satisfies \(\sum_{i,j}U_{ij}^{\prime} =1\),\(U_{ij}^\prime \geq 0\); and satisfying inequalities 24 and 25, the updated \(V_{kl}^{\prime}\) satisfies \(\sum_{l}V_{kl} =1\),\(V_{kl}^\prime \geq 0\).

Next, we determine \(\lambda^{+}\) and \(\psi_k^{+}\). First, we derive the condition of \(\lambda^{+}\) to satisfy inequality 22, which is equivalent to

\begin{align} 1 - \sum_{i,j} \frac { U_{ij} \left[\partial_{U_{ij}}L\right]^- } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } \nonumber \\ \end{align}

\begin{align} = &\sum_{i,j}U_{ij} - \sum_{i,j} \frac { U_{ij} \left[\partial_{U_{ij}}L\right]^- } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } \nonumber \\ \end{align}

\begin{align} = &\sum_{i,j} \frac { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} }U_{ij} - \sum_{i,j} \frac { U_{ij} \left[\partial_{U_{ij}}L\right]^- } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } \nonumber \\ \end{align}

\begin{align} = &\sum_{i,j} \frac { (\left[\partial_{U_{ij}}L\right]^+ - \left[\partial_{U_{ij}}L\right]^- + \lambda^{+}) U_{ij} } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } \nonumber \\ \end{align}

\begin{align} = &\sum_{i,j} \frac { \left( \partial_{U_{ij}}L + \lambda^{+} \right) U_{ij} } { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} } \nonumber \geq 0. \end{align}

Hence, by satisfying

\begin{align} \forall i,j~ \lambda^{+} \geq -\partial_{U_{ij}}L, \end{align}

inequality 22 is satisfied. Likewise, we can ensure

\begin{align} \forall l,~ \psi_k^{+} \geq -\partial_{V_{kl}}L \end{align}

which is the inequality condition for satisfying inequality 24.

Next, we determine the optimal values of \(\lambda^{+}\) and \(\psi_k^{+}\). Update rules 16 and 17 can be written as the following gradient descent manner:

\begin{align} U_{ij}^{\prime} \gets& ~U_{ij} \frac {\left[\partial_{U_{ij}}L\right]^- + \lambda^{-}} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}}\nonumber\\ &= U_{ij} - \frac {U_{ij}} {2 \left[\partial_{U_{ij}}L\right]^+ + 2\lambda^{+} } \partial_{U_{ij}}L \nonumber\\ &= U_{ij} - \eta\cdot \partial_{U_{ij}}L, \end{align}

\begin{align} V_{kl}^{\prime} \gets& ~V_{kl} \frac {\left[\partial_{V_{kl}}L\right]^- + \psi_k^{-}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}}\nonumber\\ &= V_{kl} - \frac {U_{kl}} {2 \left[\partial_{V_{kl}}L\right]^+ + 2\psi_k^{+} } \partial_{V_{kl}}L \nonumber\\ &= V_{kl} - \delta\cdot \partial_{V_{kl}}L, \end{align}

where \(\eta\) and \(\delta\) indicate the step size parameters for gradient descent. Therefore, the smaller \(\lambda^{+}\) and \(\psi_k^{+}\) leads to the larger step size. Thus, we can determine \(\lambda^{+}\) and \(\psi_k^{+}\) as follows:

\begin{align} \lambda^{+} &= \max\left(\max\left( -\partial_{U_{\cdot\cdot}}L \right),0\right), \\ \psi^{+}_k &= \max\left(\max\left(\partial _{V _{k\cdot}} L\right),0\right) \end{align}

which are the smallest value of \(\lambda^{+}\) satisfying inequalities 22 and 23, and \(\psi^{+}_k\) satisfying inequalities 24 and 25. Finally, by setting the derivatives of \(L\) to be zero, we can achieve:

\begin{align} [\partial _{U _{ij}}L]^+ &= (UVV^T) _{ij},\\ [\partial _{U _{ij}}L]^- &= (XV^T) _{ij}, \end{align}

\begin{align} [\partial _{V _{kl}}L]^+ &= (U^TUV) _{kl},\\ [\partial _{V _{kl}}L]^- &= (U^TX) _{kl}. \end{align}

B. Theoretical supports

The validity of update rules of \(U\) and \(V\) are supported by the following theorems.

Theorem 4.1: Under the update rule of \(U\), \(\sum_{i,j}U_{ij}=1\).

Proof: Under the update rule, \(\lambda^{+}\) and \(\lambda^{-}\) satisfy inequalities 22 and 23. Therefore, \(U_{ij}\) satisfies \(\sum_{i,j}U_{ij}=1\). \(\Box\)

Theorem 4.2: Under the update rule of \(V\), \(\sum_{l}V_{kl}=1\).

Proof: Under the update rule, \(\psi_k^{+}\) and \(\psi_k^{-}\) satisfy inequalities 24 and 25. Therefore, \(V_{kl}\) satisfies \(\sum_{l}V_{kl}=1\). \(\Box\)

Theorem 4.3: Under the update rule of \(U\), \(U_{ij}\geq 0\).

Proof: When \(\lambda^{+}\) and \(\lambda^{-}\) satisfy inequalities 22 and 23, \(U_{ij}\), \(\left[\partial_{U_{ij}}L\right]^+\), \(\left[\partial_{U_{ij}}L\right]^-\), \(\lambda^{+}\) and \(\lambda^{-}\) are all non negative. Thus, updated \(U_{ij}\) satisfies \(U_{ij}\geq 0\). \(\Box\)

Theorem 4.4: Under the update rule of \(V\), \(V_{kl}\geq 0\).

Proof: When \(\psi_k^{+}\) and \(\psi_k^{-}\) satisfy inequalities 24 and 25, \(V_{kl}\), \(\left[\partial_{V_{kl}}L\right]^+\), \(\left[\partial_{V_{kl}}L\right]^-\), \(\psi_k^{+}\) and \(\psi_k^{-}\) are all non negative. Thus, the updated \(V_{kl}\) satisfies \(V_{kl}\geq 0\). \(\Box\)

Theorem 4.5: When \(U_{ij}\) and \(V_{kl}\) converges, then the final solutions satisfy the KKT optimality conditions. (Proof in Appendix A.)

Theorem 4.6: Loss function \(L\) is non-increasing under the iterative update rules. (Proof in Appendix B.)

Therefore, under our proposed iterative optimization scheme, the value of loss function never increases while matrices \(U\) and \(V\) satisfy the probabilistic constraints.

C. Computational Complexity

In this section, we analyze the computational complexity of the proposed optimization algorithm. The update rules in our algorithm have the following complexities:

For update rule for \(U\).

Calculate \(\left[\partial_{U_{ij}}L\right]^+\) requires \(O(NMK)\).
Calculate \(\left[\partial_{U_{ij}}L\right]^-\) requires \(O(NMK)\).
Calculate \(\lambda\) requires \(O(NK)\).

For update rule for \(V\).

Calculate \(\left[\partial_{V_{kl}}L\right]^+\) requires \(O(NMK)\).
Calculate \(\left[\partial_{V_{kl}}L\right]^-\) requires \(O(NMK)\).
Calculate \(\psi\) requires \(O(MK)\).

In summary, update rule of our method requires the following time-complexity, where iter is the number of outer iteration:

\begin{align} O(\emph{iter}NMK) \end{align}

which is equal to the time complexity of update rule in standard NMF. Consequently, we can say that our optimization algorithm is efficient enough.

V. EXPERIMENTS

In the experiment, we evaluate our proposed optimization scheme. Specifically, we apply the proposed scheme for two different problems. One is based on a simple topic modeling over documents, described in Section III, and the other is based on a more complicated model called CARNMF [1], where community detection, attribute-value clustering, and derivation of relationships between communities and topics are simultaneously solved.

The experiments were performed on a PC with an Intel Core i7 (3.3 GHz) CPU with 16 GB RAM running macOS.

A. Topic modeling

We first discuss the results of applying the proposed optimization scheme for topic modeling based on probabilistic NMF. The evaluation criteria are as follows: (1) accuracy of topic-based clustering, (2) quality of detected topics, and (3) convergence speed of the loss function.

Experimental setting: For the dataset, two benchmark data sets [22] are employed. The first dataset is Reuters dataset. We excluded categories with less than 100 documents, resulting in 8 categories of 7,612 documents. The second dataset is 20 newsgroups dataset consisting of 20 categories, including 15,404 documents. The number of words for a dictionary is 5,000. After removing the stop words and stemming, the top of the most frequent words are selected. As the comparative methods, we employ ordinary NMF [2] and Latent Dirichlet Allocation (LDA) [23]. As for LDA, we used gensim 3.5.0 implementation of Python 3.6.3.
Document clustering: In this section, we describe the accuracy of topic-based document clustering. Clustering was performed, having obtained the topic model, we assign for each document the topic with the highest probability. Each method is applied 50 times and we measured the average accuracy and the standard deviations. To measure the performance of clustering, we use two popular metrics namely clustering accuracy (ACC) and normalized mutual information (NMI) [4]. The results are summarized in Tables I and II. These results show that the proposed probabilistic NMF achieved higher NMI and ACC in both Reuters and 20 newsgroups. This indicates that probabilistic NMF detects clusters more accurately than clustering based on ordinary NMF and LDA.

TABLE I: NMI scores

dataset	Reuters	20 newsgroups
LDA	22.99 ± 5.90	14.01 ± 2.20
NMF	36.75 ± 1.15	29.01 ± 1.95
Probabilistic NMF	37.70 ± 0.98	30.90 ± 1.92

TABLE II: ACC scores

dataset	Reuters	20 newsgroups
LDA	46.11 ± 8.38	18.18 ± 1.500
NMF	52.97 ± 1.47	30.67 ± 2.97
Probabilistic NMF	53.78 ± 1.76	32.93 ± 3.24

Topic Modeling: We examined the quality of topics detected by various methods. As an evaluation metrics, we employed coherence [24], where higher coherence score indicates better consistent with human judgments on topic qualities. We varied the top-N words for calculating the coherence score. In order to investigate the overall quality of the discovered topic set, we use the average topic coherence score. Tables III and IV are the coherence scores for Reuters dataset and 20 newsgroups dataset respectively. These tables show that, in most cases, our probabilistic NMF achieves higher coherence than the baselines. These results imply that probanilistic NMF achieves more reasonable topic modeling than the baselines.
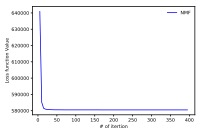
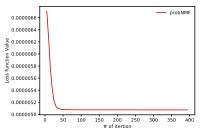
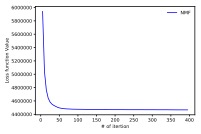
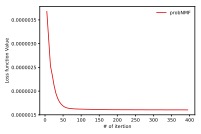
Convergence speed of optimization: In this section, we examine the convergence and learning efficiency of the proposed optimization scheme. In this experiment, we set the number of topics to 8 for Reuters dataset and 20 for 20 newsgroups dataset. In Figures 1, we plotted the loss function value in each iteration step for the ordinary NMF and the proposed probabilistic NMF. These figures show that our optimization scheme monotonically decreases the loss function. Moreover, probabilistic NMF converges as fast as the ordinary NMF. The running times of ordinary NMF on the Reuters (20 newsgroups) dataset are 0.425 ± 0.015s (3.12 ± 0.16s) and probabilistic NMF are 0.585 ± 0.030s (3.64 ± 0.19). These results imply that our optimization scheme does not incur extra cost and can be practically used as ordinary NMF.

TABLE III: Coherence scores on Reuters dataset.

Top N words	5	10	20	50
LDA	-4.98 ± 4.90	-31.04 ± 1.61	-165.86 ± 6.30	-1315.49 ± 34.87
NMF	-5.07 ± 0.20	-28.70 ± 0.62	-151.05 ± 3.15	-1263.84 ± 26.44
Probabilistic NMF	-5.16 ± 0.18	-29.08 ± 0.65	-152.01 ± 3.55	-1236.05 ± 20.84

TABLE IV: Coherence scores on 20 newsgroups dataset.

Top N words	5	10	20	50
LDA	-7.42 ± 0.63	-39.78 ± 2.10	-190.20 ± 5.62	-1382.11 ± 26.37
NMF	-6.49 ± 0.32	-37.57 ± 1.31	-186.78 ± 5.50	-1361.01 ± 30.97
Probabilistic NMF	-6.29 ± 0.20	-36.22 ± 0.49	-180.29 ± 3.06	-1316.37 ± 17.69

(a) NMF Reuters

(b) Probabilistic NMF Reuters

(d) Probabilistic NMF 20 newsgroups

Fig. 1: Loss function value under iterations.

B. More complicated model

In this section, we examine the effectiveness of our optimization scheme by applying to more complicated NMF based model called CARNMF. CARNMF is a clustering method for multi-attributed graphs which detects (1) community of nodes, (2) cluster of attribute values, and (3) relationships between communities and clusters of attributes. The loss function of CARNMF is as follows:

\begin{align} \argmin _{U^{\star}, {{\lbrace U^{(t)}, V^{(t)}, R^{(t)} \rbrace _{t \in \mathbb{T}} }\geq 0}} L = \left\lVert A-U^\star(U^\star)^T \right\rVert ^2_F \nonumber \\ + \sum _{t \in \mathbb{T}} \lbrace \left\lVert X^{(t)}-U^{(t)}(V^{(t)})^T \right\rVert ^2_F + \lambda_t \left\lVert U^{(t)}-U^*R^{(t)} \right\rVert ^2_F \rbrace \\ \end{align}

\begin{align} s.t. ~~ \forall 1 \leq r \leq k_t, \forall 1 \leq p \leq \ell, \forall t \in {\mathbb T}, \nonumber \end{align}

\begin{align} \sum _{i,j} U^\star _{ij} = 1, \sum _{i,j} U^{(t)} _{ij} = 1, \sum _{i} V^{(t)} _{ir} = 1, \sum _{j} R^{(t)} _{pj} = 1, \nonumber \end{align}

\noindent where \(A\) and \(\left\{X^{(t)}\right\}_{t\in{\mathbb T}}\) represents multi-attributed graph which is an input of the method; each element \(A_{u,v}\) of \(A\) indicates the joint probability \(p(u,v)\) of edge presence between nodes \(u\) and \(v\),each element \(X^{(t)}_{u,x}\) of \(X^{(t)}\) indicates the joint probability \(p(u,x)\) of edge presence between a node \(u\) and an attribute value of \(t\)-th attribute \(x\). \(U^*\), \(U^{(t)}\), \(V^{(t)}\), and \(R^{(t)}\) are the output matrices. Each element \(U^*_{u,c}\) of \(U^*\) indicates the joint probability \(p(u,c)\) of a node \(u\) belongs to a community \(c\). Each element \(U^{(t)}_{u,s^{(t)}}\) of \(U^{(t)}\) indicates the joint probability \(p(u,s^{(t)})\) of a node \(u\) relates to a cluster of \(t\)-th attribute \(s^{(t)}\). Each element \(V^{(t)}_{x,s^{(t)}}\) of \(V^{(t)}\) indicates the conditional probability \(p(x|s^{(t)})\) of a cluster \(s^{(t)}\) has an attribute \(x\). Each element \(R^{(t)}_{c,s^{(t)}}\) of \(R^{(t)}\) indicates the conditional probability \(p(s^{(t)}|c)\) of a community \(c\) relates to a cluster \(s^{(t)}\). \(\lambda_t\) is a hyper parameter which controls the effect of \(t\)-th attribute. For more detailed description, please refer to the original paper.

CARNMF achieves higher accuracy by collaborating with the community detection and attribute-value clustering. In the original paper, an optimization algorithm for the loss function has been proposed. However, the output matrices do not always satisfy the probabilistic constraints under the optimization process.

We derive update rules for each of output matrices based on the proposed optimization scheme. The matrices \(U^*\) and \(U^{(t)}\) has constraint \(\sum_{i,j}U^*_{i,j}=1\) and \(\sum_{i,j}U^{(t)}_{i,j}=1\) respectively, thus we use the update rule of \(U\). The matrices \(U^{(t)}\) and \(R^{(t)}\) has constraint \(\sum_{j}V^{(t)}_{\cdot,j}=1\) and \(\sum_{j}R^{(t)}_{\cdot,j}=1\) respectively, thus we use the update rule of \(V\). The derivatives of each matrix are the following:

\begin{align} [\partial_{U^*}L]^+ =& 2U^\star(U^{\star})^TU^\star +\sum_{t \in \mathbb{T}} \lambda_t U^\star R^{(t)}(R^{(t)})^T,\\ \end{align}

\begin{align} [\partial_{U^\star}L]^- =& 2A^TRU^\star +\sum_{t \in \mathbb{T}}U^{(t)}(R^{(t)})^T \ \end{align}

\begin{align} [\partial_{U^{(t)}}L]^+ =& U^{(t)}(V^{(t)})^TV^{(t)} +\lambda_t U^{(t)},\\ \end{align}

\begin{align} [\partial _{U^{(t)}}L]^{-} =& X^{(t)} V^{(t)} +\lambda _t U^{\star} R^{(t)}, \ \end{align}

\begin{align} [\partial_{V^{(t)}}L]^+ =& (V^{(t)})^T(U^{(t)})^TU^{(t)},\\ \end{align}

\begin{align} [\partial_{V^{(t)}}L]^- =& (X^{(t)})^TU^{(t)},\\ \end{align}

\begin{align} [\partial_{R_i}L]^+ =& (U^{\star})^TU^*R^{(t)},\\ \end{align}

\begin{align} [\partial_{R_i}L]^- =& (U^{\star})^TU^{(t)}. \end{align}

In this experiment, the accuracy of clustering is verified using DBLP and arXiv of the bibliographic database. Specifically, the detection accuracy of the node (author), the paper, conference/journal attribute detection accuracy was verified. The setting of the experiment follows the setting of Ito et al. [1]. Table V summarizes the clustering accuracy. probCARNMF is the result of optimizing CARNMF with this optimization method. It can be seen that the accuracy is improved by optimization by this optimization method. This indicates that modeling of communities and attribute-value clusters has become more reasonable.

TABLE V: Accuracy of community detection and attribute clustering.

|(1) DBLP dataset|(2) arXiv dataset|

Methods	Author	Paper	Conference	Author	Paper	Journal
NMF(A-T)	64.02 ± 5.73	N/A	N/A	60.99 ± 0.07	N/A	N/A
NMF(A-P)	43.12 ± 5.17	44.58 ± 5.89	N/A	44.84 ± 5.06	30.94 ± 1.15	N/A
NMF(A-C)	75.35 ± 6.85	N/A	87.60 ± 1.73	75.85 ± 7.29	N/A	73.68 ± 2.33
NMF(T-P)	N/A	50.02 ± 7.93	N/A	N/A	39.80 ± 5.05	N/A
NMF(T-C)	N/A	N/A	69.88 ± 6.68	N/A	N/A	100.00 ± 0.0
LCTA [25]	48.90 ± 7.57	26.13 ± 4.36	68.50 ± 12.46	46.72 ± 5.72	31.50 ± 1.17	56.87 ± 6.53
SCI [14]	54.78 ± 8.79	22.31 ± 1.48	58.20 ± 7.40	35.42 ± 4.01	29.79 ± 1.11	47.49 ± 6.37
HINMF [15]	68.90 ± 9.08	56.46 ± 3.08	90.10 ± 12.63	74.30 ± 7.99	29.68 ± 0.95	73.12 ± 8.86
CARNMF [1]	86.34 ± 2.39	78.19 ± 9.87	97.20 ± 5.21	77.64 ± 2.88	44.05 ± 3.14	75.00 ± 5.23
probCARNMF	88.56 ± 1.62	79.28 ± 5.83	100.00 ± 0.0	83.42 ± 0.0	47.84 ± 0.71	87.50 ± 0.0

VI. CONCLUSIONS AND FUTURE WORK

In this paper, we have proposed a novel optimization method for NMF under probabilistic constraint called \textit{probabilistic NMF}, whereby the output matrices are interpretable as probability matrices without any operation such as normalization. We have exploited topic modeling as an example of probabilistic NMF and derived an iterative optimization algorithm for it. For the method, we have given theoretical supports for the validity of update rules: (1) our optimization scheme monotonically decrease the objective function; (2) the output matrices always meet the probability constraints; (3) the learning rate of update rules for each output matrix is the maximum under satisfying (1) and (2); and (4)the time complexity of the proposed optimization scheme remains the same as the ordinary NMF. The experimental results have shown that, when applying it to topic modeling under probabilistic NMF, the model optimized by our optimization scheme is more accurate than the ordinary NMF regarding clustering and topic detection without sacrificing efficiency compared with ordinary NMF. Moreover, another experimental results regarding CARNMF showed that we achieve more accurate communities and attribute-value clusters than the original optimization algorithm.

As for future work, many research directions are conceivable. First, we consider our optimization schemes for NMF under any other kind of distance metrics such as Kullback-Leibler (KL) divergence, Itakura-Saito (IS) divergence [26], and \(\ell_{2,1}\) norms. Second, we examine the effect of regularization terms for probabilistic NMF such as \(\ell_1\), \(\ell_2\) based regularization [27], and manifold regularization [28]. Third, we try to find the connections between probabilistic NMF and probabilistic models, that leads theoretical views of the method.

APPENDIX

A. Proof of Theorem 4.5

Proof: At convergence, \(U_{ij}^{(\infty)}=U_{ij}^{(t+1)}=U_{ij}^{(t)}=U_{ij}\), \(V_{kl}^{(\infty)}=V_{kl}^{(t+1)}=V_{kl}^{(t)}=V_{kl}\), where \(t\) denotes the \(t\)-th iteration, i.e.,

\begin{align} U_{ij}= U_{ij} \frac {\left[\partial_{U_{ij}}L\right]^- + \lambda^{-}} {\left[\partial_{U_{ij}}L\right]^+ + \lambda^{+}},~~ V_{kl}= V_{kl} \frac {\left[\partial_{V_{kl}}L\right]^- + \psi_k^{-}} {\left[\partial_{V_{kl}}L\right]^+ + \psi_k^{+}},\nonumber \end{align}

which are equivalent to

\begin{align} U_{ij}\left( \left[\partial_{U_{ij}}L\right]^+ - \left[\partial_{U_{ij}}L\right]^- +\lambda^{+} - \lambda^{-}\right) =0, \nonumber\\ V_{kl} \left( \left[\partial_{V_{kl}}L\right]^+ - \left[\partial_{V_{kl}}L\right]^- + \psi_k^{+} - \psi_k^{-}\right) =0, \nonumber \end{align}

which are equivalent to Eq. 14 and Eq. 15, respectively. \(\Box\)

B. Proofs of Theorem 4.6

In this section, we give a proof of Theorem 4.6. Due to the space limitation, we only prove that the update rule of \(U\) does not increase the loss function \(L\). We can prove for \(V\) as the similar fashion. We will follow the similar aproach described in [28] which utilize the property of the auxiliary function. We let \(L(U_{ij})\) be the loss function \(L\) with \(U_{ij}\) as a variable.

Definition A.1: \(G(U_{ij},U_{ij}^{\prime})\) is an auxiliary function for \(L(U_{ij})\) if the conditions

\begin{align} G(U_{ij},U_{ij}^{\prime}) \geq L\left(U_{ij}\right), ~~~~ G(U_{ij},U_{ij})=L(U_{ij}) \nonumber \end{align}

are satisfied.

Lemma A.1: If \(G\) is an auxiliary function of \(F\), then \(F\) is non-increasing under the update

\begin{align} U_{ij}^{\prime} = \argmin_{U_{ij}} G\left(U_{ij},U_{ij}^{(t)}\right). \end{align}

Proof: \begin{align} L\left(U_{ij} ^ {\prime} \right) \leq G \left(U_{ij}^{\prime} , U_{ij} ^ { ( t ) } \right) \leq G \left( U_{ij} ^ { ( t ) } , U_{ij} ^ { ( t ) } \right) = L \left( U_{ij} ^ { ( t ) } \right).~\Box \nonumber \end{align}

Lemma A.2: Function \begin{equation} \left. \begin{array} { r l } { G \left(U_{ij}, U_{ij}^{(t)}\right) = L\left(U_{ij}^{(t)}\right) + \partial_{U_{ij}}L\left(U_{ij}^{(t)}\right) ( U_{ij} - U_{ij}^{(t)} ) } \\ { + \frac {\left[\partial_{U_{ij}}L\right]^+ +\lambda^{+}} {U_{ij}^{(t)}} ( U_{ij} - U_{ij}^{(t)} )^{2}} \end{array} \right. \end{equation}

is an auxiliary function for \(L\).

Proof: \(G(U_{ij},U_{ij})=L(U_{ij})\) is obvious. We need to show that \(G(U_{ij},U_{ij}^{(t)}) \geq L\left(U_{ij}\right)\). To do this, we compare the Taylor series expansion of \(L\left(U_{ij}\right)\)

\begin{equation} \left. \begin{array} { r l } { L\left(U_{ij}\right) = L\left(U_{ij}^{(t)}\right) + \partial_{U_{ij}}L \left(U_{ij}^{(t)}\right) ( U_{ij} - U_{ij}^{(t)} ) } \\ { + (\partial_{U_{ij}})^2L \left(U_{ij}^{(t)}\right) ( U_{ij} - U_{ij}^{(t)} )^{2}}\end{array} \right. \end{equation}

with Eq. 47 to find that \(G(U_{ij},U_{ij}^{\prime}) \geq L\left(U_{ij}\right)\) is equivalent to

\begin{align} \frac {\left[\partial_{U_{ij}}L\right]^+ +\lambda^{+}} {U_{ij}^{(t)}} \geq (\partial_{U_{ij}})^2L. \end{align}

We have

\begin{align} \left[\partial _{U _{ij}}L\right]^+ = (UV^TV) _{ij} = \sum_k U _{ik}^{(t)} (V^TV) _{kj} \nonumber\\ \geq U^{(t)} _{ij} (V^TV) _{jj} = U^{(t)} _{ij} (\partial _{U _{ij}})^2L. \nonumber \end{align}

Therefore, inequality 49 holds and \(G(U_{ij},U_{ij}^{(t)}) \geq L\left(U_{ij}\right)\). \(\Box\)

Proof of Theorem1: Replacing \(G \left(U_{ij}, U_{ij}^{(t)}\right)\) in equation 46 by equation 47 results in the update rule:

\begin{align} U_{ij}^{\prime} &= U_{ij}^{(t)} - U_{ij}^{(t)} \frac {\partial_{U_{ij}}L} {2 \left[\partial_{U_{ij}}L\right]^+ + 2\lambda^{+} } \nonumber\\ &= U_{ij}^{(t)} \frac { \left[\partial_{U_{ij}}L\right]^- + \lambda^{-}} { \left[\partial_{U_{ij}}L\right]^+ + \lambda^{+} }. \end{align}

Since equation 47 is an auxiliary function, \(L\) is non increasing under this update rule. \(\Box\)

ACKNOWLEDGMENT

This work was supported by C-AIR Cooperative Research Project of Center for Artificial Intelligence Research, University of Tsukuba.

REFERENCES

[1] H. Ito, T. Komamizu, T. Amagasa, and H. Kitagawa, “Community detection and correlated attribute cluster analysis on multi-attributed graphs,” in Proceedings of the Workshops of the EDBT/ICDT 2018 Joint Conference (EDBT/ICDT 2018), Vienna, Austria, March 26, 2018., 2018, pp. 2–9. [Online]. Available: http://ceur-ws.org/Vol-2083/paper-01.pdf
[2] D. D. Lee and H. S. Seung, “Algorithms for non-negative matrix factorization,” in Advances in neural information processing systems, 2001, pp. 556–562.
[3] ——, “Learning the parts of objects by non-negative matrix factorization,” Nature, vol. 401, no. 6755, pp. 788–791, 1999.
[4] W. Xu, X. Liu, and Y. Gong, “Document clustering based on non-negative matrix factorization,” in SIGIR 2003: Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Toronto, Canada, 2003, pp. 267–273.
[5] C. Ding, T. Li, W. Peng, and H. Park, “Orthogonal nonnegative matrix t-factorizations for clustering,” in Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2006, pp. 126–135.
[6] T. Shi, K. Kang, J. Choo, and C. K. Reddy, “Short-text topic modeling via non-negative matrix factorization enriched with local word-context correlations,” in Proceedings of the 2018 World Wide Web Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 2018, pp. 1105–1114.
[7] H. Kim, J. Choo, J. Kim, C. K. Reddy, and H. Park, “Simultaneous discovery of common and discriminative topics via joint nonnegative matrix factorization,” in Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2015, pp. 567–576.
[8] J. Choo, C. Lee, C. K. Reddy, and H. Park, “Utopian: User-driven topic modeling based on interactive nonnegative matrix factorization,” IEEE Transactions on Visualization and Computer graphics, vol. 19, no. 12, pp. 1992–2001, 2013.
[9] J. Yang and J. Leskovec, “Overlapping community detection at scale: a nonnegative matrix factorization approach,” in Proceedings of the sixth ACM international conference on Web search and data mining. ACM, 2013, pp. 587–596.
[10] D. Kuang, C. Ding, and H. Park, “Symmetric nonnegative matrix factorization for graph clustering,” in Proceedings of the 2012 SIAM International Conference on Data Mining. SIAM, 2012, pp. 106–117.
[11] Y. P. N. Chakraborty and K. Sycara, “Nonnegative matrix tri-factorization with graph regularization for community detection in social networks,” in Proceedings of the Twenty-Third international joint conference on Artificial Intelligence, 2015, pp. 2083–2089.
[12] F. Wang, T. Li, X. Wang, S. Zhu, and C. Ding, “Community discovery using nonnegative matrix factorization,” Data Mining and Knowledge Discovery, vol. 22, no. 3, pp. 493–521, 2011.
[13] P. Smaragdis, “Non-negative matrix factor deconvolution; extraction of multiple sound sources from monophonic inputs,” in Independent Component Analysis and Blind Signal Separation. Springer, 2004, pp.494–499.
[14] X. Wang, D. Jin, X. Cao, L. Yang, and W. Zhang, “Semantic community identification in large attribute networks,” in AAAI, 2016, pp. 265–271.
[15] J. Liu and J. Han, “Hinmf: A matrix factorization method for clustering in heterogeneous information networks,” in Proceedings of the interna- tional joint conference on artificial intelligence workshop, 2013.
[16] J. Liu, C. Wang, J. Gao, and J. Han, “Multi-view clustering via joint nonnegative matrix factorization,” in Proceedings of the 2013 SIAM International Conference on Data Mining. SIAM, 2013, pp. 252–260.
[17] D. Guillamet and J. Vitrià, “Non-negative matrix factorization for face recognition,” in Topics in artificial intelligence. Springer, 2002, pp. 336–344.
[18] C. Ding, T. Li, and W. Peng, “Nonnegative matrix factorization and probabilistic latent semantic indexing: Equivalence chi-square statistic, and a hybrid method,” in AAAI, vol. 42, 2006, pp. 137–143.
[19] ——, “On the equivalence between non-negative matrix factorization and probabilistic latent semantic indexing,” Computational Statistics & Data Analysis, vol. 52, no. 8, pp. 3913–3927, 2008.
[20] E. Gaussier and C. Goutte, “Relation between plsa and nmf and implications,” in Proceedings of the 28th annual international ACM SIGIR conference on Research and development in information retrieval. ACM, 2005, pp. 601–602.
[21] M. Luo, F. Nie, X. Chang, Y. Yang, A. G. Hauptmann, and Q. Zheng, “Probabilistic non-negative matrix factorization and its robust extensions for topic modeling.” in AAAI, 2017, pp. 2308–2314.
[22] D. Cai and X. He, “Manifold adaptive experimental design for text categorization,” IEEE Transactions on Knowledge and Data Engineering, vol. 24, no. 4, pp. 707–719, 2012.
[23] D. M. Blei, A. Y. Ng, and M. I. Jordan, “Latent dirichlet allocation,” Journal of Machine Learning Research, vol. 3, pp. 993–1022, 2003.
[24] D. Mimno, H. M. Wallach, E. Talley, M. Leenders, and A. McCallum, “Optimizing semantic coherence in topic models,” in Proceedings of the conference on empirical methods in natural language processing. Association for Computational Linguistics, 2011, pp. 262–272.
[25] Z. Yin, L. Cao, Q. Gu, and J. Han, “Latent community topic analysis: integration of community discovery with topic modeling,” ACM Transactions on Intelligent Systems and Technology (TIST), vol. 3, no. 4, p. 63, 2012.
[26] C. Févotte and A. T. Cemgil, “Nonnegative matrix factorizations as probabilistic inference in composite models,” in Signal Processing Conference, 2009 17th European. IEEE, 2009, pp. 1913–1917.
[27] L. Xing, H. Dong, W. Jiang, and K. Tang, “Nonnegative matrix factorization by joint locality-constrained and 2, 1-norm regularization,” Multimedia Tools and Applications, vol. 77, no. 3, pp. 3029–3048, 2018.
[28] D. Cai, X. He, J. Han, and T. S. Huang, “Graph regularized nonnegative matrix factorization for data representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 8, pp. 1548–1560, 2011.